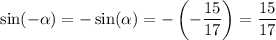Starting from the fundamental trigonometric equation, we have

Since
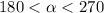 , we know that the angle lies in the third quadrant, where both sine and cosine are negative. So, in this specific case, we have
, we know that the angle lies in the third quadrant, where both sine and cosine are negative. So, in this specific case, we have
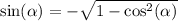
Plugging the numbers, we have
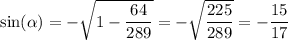
Now, just recall that
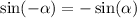
to deduce