Answer:
Explanation:
First thing we need to do is to reconcile that r to the negative power. You do that by following the rules for exponents. If
 then the rule is to subtract the lower exponent from the upper:
then the rule is to subtract the lower exponent from the upper:
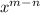
Doing that with our base of r:
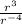 is
is
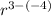 which is
which is
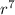
So it looks like what we have now is:
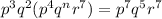
NOW we will follow the rules for multiplying like bases with exponents. The rule for that is if you have like bases and you are multiplying those like bases, you add the exponents. So I'm going to kind of break up that problem and put the like bases together:
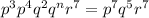
Working on the left side, p to the 3rd times p to the 4 gives you p to the 7th, which is what we have on the right. The r to the 7 is also the same on the left and the right. Working on the q's now, if we have q to the 2nd and we are looking for n, then
 so 2 + n = 5 and n = 3
so 2 + n = 5 and n = 3