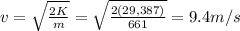Answer:
9.4 m/s
Step-by-step explanation:
The work-energy theorem states that the work done on an object is equal to the change in kinetic energy of the object.
So we can write:
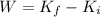
where in this problem:
W = -36.733 J is the work performed on the car (negative because its direction is opposite to the motion of the car)
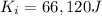 is the initial kinetic energy of the car
is the initial kinetic energy of the car
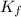 is the final kinetic energy
is the final kinetic energy
Solving for Kf,
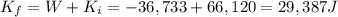
The kinetic energy of the car can be also written as
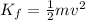
where:
m = 661 kg is the mass of the car
v is its final speed
Solving, we find