Answer: 162.024 square centimeters
Explanation:
We know that , the shape of a can is cylinder .
Given , Height of can = 6 cm
Radius of can = 4.3 cm
We know that , the lateral surface area of cylinder=
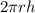
Let
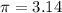
Then, the lateral surface area of can =
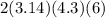
=162.024 square centimeters
Hence, the lateral surface area of the label of the soup can is 162.024 square centimeters.