Question

A label wraps around soup can with a radius of 4.3 cm and a height of 6 cm. What is the lateral surface area of the label of the soup can in square centimeters?

Answer 1

Answer: 162.024 square centimeters

Explanation:

We know that , the shape of a can is cylinder .

Given , Height of can = 6 cm

Radius of can = 4.3 cm

We know that , the lateral surface area of cylinder=
`2\pi rh`

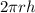
Let
`\pi=3.14`

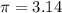
Then, the lateral surface area of can =
`2(3.14)(4.3)(6)`

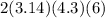
=162.024 square centimeters

Hence, the lateral surface area of the label of the soup can is 162.024 square centimeters.

Answer 2

`52\pi \text{ cm}^2\approx 162.11\text{ cm}^2`

Explanation:

We have been given that a label wraps around soup can with a radius of 4.3 cm and a height of 6 cm. We are asked to find the lateral surface area of the label of the soup can in square centimeters.

We will use lateral surface area of cylinder to solve our given problem as:

`LA=2\pi rh`, where,

r = Radius of cylinder,

h = height of cylinder.

Upon substituting our given values in above formula, we will get:

`LA=2\pi *\text{4.3 cm}* \text{6 cm}`

`LA=51.6\pi \text{ cm}^2`

`LA=162.10618\text{ cm}^2`

Therefore, the lateral surface area of the label of the soup is approximately 162.11 square cm.