Sam has a jar contain 80 coins, all of which are either quarters or nickels. The total value of the coins is $14.60. How many of each type of coin does she have?

Question

asked Aug 7, 2021 110k views

1 Answer

Pihentagy · Answer 1 · 2021-08-14T08:52:02+0000

Answer:

She have 53 type of quarters and 27 type of nickels.

Explanation:

Given:

Sam has a jar contain 80 coins, all of which are either quarters or nickels.

The total value of quarters and nickels is $14.60.

Now, to get each type of coin she have.

Let the number of quarters be

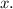
And let the number of nickels be

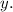
So, total number of coins:

x+y=80

$y=80-x\ \ \ ....(1)$

Now, the total value of coins:

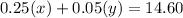
0.25(x)+0.05(y)=14.60

Substituting the value of
from equation (1):

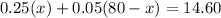
0.25(x)+0.05(80-x)=14.60

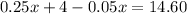
0.25x+4-0.05x=14.60

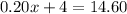
0.20x+4=14.60

Subtracting both sides by 4 we get:

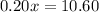
0.20x=10.60

Dividing both sides by 0.20 we get:

x=53.

The number of quarters = 53.

Now, to get the number of nickels by substituting the value of
in equation (1):

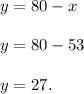
$y=80-x\\\\y=80-53\\\\y=27.$

The number of nickels = 27.

Therefore, she have 53 type of quarters and 27 type of nickels.