Answer:
a. Ameribank-$15,157.50
b. Capital Two-$4,646.25
Explanation:
a. Tad's savings is $15,000, we calculate his total amount at the end of the year for each bank:
#Ameribank
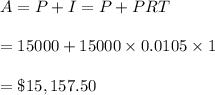
#Huffington( we use the effective rate to calculate the compound amount):
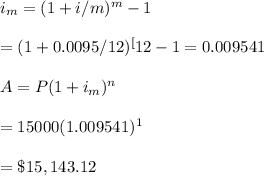
#Sixth-Third, Take 1 yrs=52 weeks:
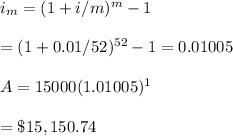
#Hence, Ameribank is the best option as his money grows to $15,157.50 which is greater than all the remaining two options.
b. We use the compound interest formula
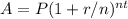 to determine which bank gives the best option:
to determine which bank gives the best option:
#Capital Two. r=3.75%, n=12,t=4
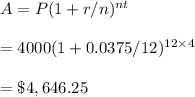
#J.C Morgan, t=2, r=3.55% n=12
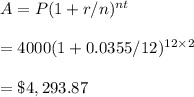
#Silverman Slacks, n=12,t=3, r=3.65%
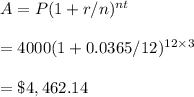
We compare the investment amounts after t years:
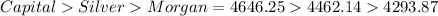
Hence, Capital two is the best option with an investment amount of $4,646.25