Question

Suppose that, for a particular social networking company, the annual revenue from rich media advertisements, in millions of dollars, for the years 2007 through 2012 can be approximated with the model R ( x ) = − x^4 + 8 x^3 − 38 x^2 + 44x , where x is the number of years from the beginning of 2007.

a. For this company, what was the revenue from rich media advertisements at the beginning of 2010?

B. At what rate was the revenue changing in the year 2010?

Answer 1

a. Revenue of the company at the beginning of 2010 is 75 million dollar (loss)

b. Rate at which the revenue changing in the year 2010 is 76 million dollar per year ( decreasing)

Explanation:

For part a,

Given that x is the number of years at the beginning of 2007.

Therefore,
`x=0` for year 2007.

Hence at the year 2010 value of x will be
`x=3`.

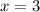Substitute the value of x=3 in R(x),

`R\left(x\right)=-x^(4)+8x^(3)-38x^(2)+44x`

`R\left(x\right)=-\left(81\right)+8\left(27\right)-38\left(9\right)+132`

`R\left(x\right)=-81+216-342+132`

`R\left(x\right)=-75`

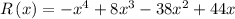
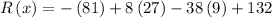
Negative sign indicates that there is loss of revenue at the start of the year 2010

Therefore, there is loss of revenue at the beginning of 2010 which is 75 million dollar.

For part b,

To calculate rate, differentiate the given function with respect to x.

`(d)/(dx)R\left(x\right)=(d)/(dx)\left (-\left(x\right)^(4)+8\left(x\right)^(3)-38\left(x\right)^(2)+44\left(x\right)\right)`

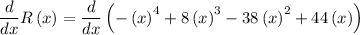
Applying sum and difference rule of derivative,

`(d)/(dx)R\left(x\right)=-(d)/(dx)\left(x^4\right)+(d)/(dx)\left(8x^3\right)-(d)/(dx)\left(38x^2\right)+(d)/(dx)\left(44x\right)`

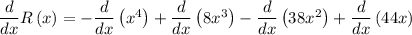
Applying constant multiple rule of derivative,

`(d)/(dx)R\left(x\right)=-(d)/(dx)\left(x^4\right)+8(d)/(dx)\left(x^3\right)-38(d)/(dx)\left(x^2\right)+44(d)/(dx)\left(x\right)`

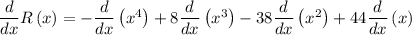
Applying power rule of derivative,

`(d)/(dx)R\left(x\right)=-\left(4x^(4-1)\right)+8\left(3x^(3-1)\right)-38\left(2x^(2-1)\right)+44\left(1x^(1-1)\right)`

`(d)/(dx)R\left(x\right)=-4\left(x^(3)\right)+8\left(3x^(2)\right)-38\left(2x^(1)\right)+44`

`(d)/(dx)R\left(x\right)=-4x^3+24x^2-76x+44`

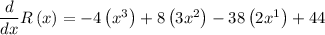
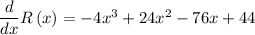
Substituting the value x=3,

`(d)/(dx)R\left(x\right)=-4\left(3\right)^3+24\left(3\right)^2-76\left(3\right)+44`

`(d)/(dx)R\left(x\right)=-4\left(27\right)+24\left(9\right)-76\left(3\right)+44`

`(d)/(dx)R\left(x\right)=-108+216-228+44`

`(d)/(dx)R\left(x\right)=-76`

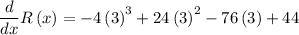
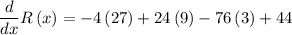
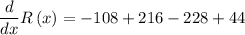
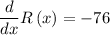
Negative sign indicates that rate is decreasing.

Rate at which the revenue is changing in the year 2010 is 76 million dollar per year.