Answer:
width = 3ft
volume = 144 ft³
Explanation:
Pythagoras Theorem
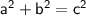
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
The diagonal of the base of the aquarium, its height, and the length from the top corner to the opposite bottom corner forms a right triangle. As we know two of the lengths, we can use Pythagoras Theorem to calculate the unknown length (diagonal of base).
Given:
- a = height of aquarium = 12 ft
- b = diagonal of base
- c = top corner to opposite corner = 13 ft
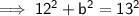
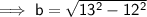
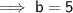
Now we know the length of the diagonal of the base, we can again use Pythagoras Theorem to find the width of the aquarium.
Given:
- a = length of aquarium = 4 ft
- b = width of aquarium
- c = diagonal of base = 5 ft
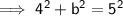
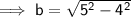
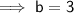
Therefore, the width of the aquarium is 3 ft.
As the aquarium is modeled as a rectangular prism:
