Question

A random sample of 29 delivered was chosen and the standard deviation of these delivery times was found to be 15.81 minutes. What is the probability that the average delivery time of the selected delivered at most 21 minutes?

Answer 1

0.5252 is the required probability.

Explanation:

The attached image shows the missing information of the question.

We are given the following information in the question:

Mean, μ = 20 minutes

Sample standard Deviation, s = 15.81 minutes

Sample size, n = 29

We are given that the distribution of delivery time is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(s)`

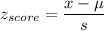
P(delivery time is atmost 21 minutes)

`P( x \leq 21) = P( z \leq \displaystyle(21 - 20)/(15.81)) = P(z \leq  0.0632)`

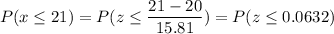
Calculation the value from standard normal z table, we have,

`P(x \leq 21) =0.5252 = 52.52\%`

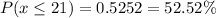
o.5252 is the probability that the average delivery time of the selected delivered at most 21 minutes.