Answer:
0.5252 is the required probability.
Explanation:
The attached image shows the missing information of the question.
We are given the following information in the question:
Mean, μ = 20 minutes
Sample standard Deviation, s = 15.81 minutes
Sample size, n = 29
We are given that the distribution of delivery time is a bell shaped distribution that is a normal distribution.
Formula:
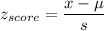
P(delivery time is atmost 21 minutes)
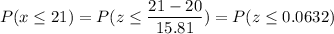
Calculation the value from standard normal z table, we have,
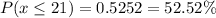
o.5252 is the probability that the average delivery time of the selected delivered at most 21 minutes.