Question

The amount of time it takes Annie to make dinner is continuous and uniformly distributed between 19 minutes and 49 minutes. What is the probability that it takes Annie between 39 and 40 minutes given that it takes less than 44 minutes for her to make dinner

Answer 1

The probability that it takes Annie between 39 and 40 minutes given that it takes less than 44 minutes for her to make dinner is 0.04.

Explanation:

Let X = amount of times (in minutes) it takes Annie to make dinner.

The random variable X follows a continuous Uniform distribution with parameters a = 19 minutes and b = 49 minutes.

The probability density function of continuous Uniform distribution is:

`f_(X)(x)=(1)/(b-a);\ a<X<b, a<b`

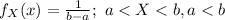
Compute the value P (39 < X < 40 | X < 44) as follows:

`P(39<X<40|X<44)=(P(39<X<40\ \cap \ X<44))/(P(X<44))=(P(39<X<40))/(X<44))`

`=\frac{\int\limits^(40)_(39) {(1)/(49-19)}\, dx}{\int\limits^(44)_(19) {(1)/(49-19)}\, dx}`

`=( (1)/(30)|x|^(40)_(39))/((1)/(30)|x|^(44)_(19))`

`=( (1)/(30)* 1)/((1)/(30)* 25)`

`=(1)/(25)`

`=0.04`

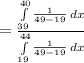
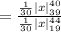
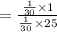
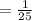
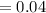
Thus, the probability that it takes Annie between 39 and 40 minutes given that it takes less than 44 minutes for her to make dinner is 0.04.