Question

An insurance company claims the average car on the road is less than 6 years old. Based on a random sample of 15 cars, the mean age is 5.8 years with a standard deviation of 1.1 years. Does the sample support the insurance company's claim?

Answer 1

Answer: No, we do not have enough evidence to support the insurance company's claim.

Explanation:

Let
`\mu` be the average car on the road .

As per given , we have

Null hypothesis :
`H_0:\mu\geq6`

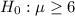
Alternative hypothesis :
`H_a:\mu<6`

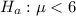
Since ,
`H_a` is left-talied and population standard deviation is unknown , so we perform a left-tailed t-test.

Test statistic :
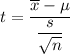`t=\frac{\overline{x}-\mu}{(s)/(√(n))}` , where
`\overline{x}`= sample mean , s= sample standard deviation , n= sample size .

Put
`\overline{x}`= 5.8 years , s= 1.1 years , n= 15 .

`t=(5.8-6)/((1.1)/(√(15)))\approx-0.704`

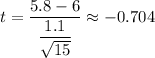
Also, At 0.05 significance ,

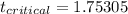`t_(critical)=1.75305` (by t-distribution table)

Decision : Since
`|t_(calculated)|<|t_(critical)| \ [\ \because\ 0.704<1.75305]` , so we fail to reject the null hypothesis .

Conclusion : At 5% confidence level , we do not have enough evidence to support the insurance company's claim.