Question

If f(1)=2f(1)=2 and f(n)=f(n-1)^2-n

then find the value of f(4)

Answer 1

Given that
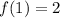`f(1)=2` and
`f(n)=[f(n-1)]^2-n`

We need to determine the value of f(4)

To determine the value of f(4), we need to know the values of the previous terms f(2), f(3).

The value of f(2):

The value of f(2) can be determined by substituting n = 2 in the function
`f(n)=[f(n-1)]^2-n`

Thus, we get;

`f(2)=[f(2-1)]^2-2`

`f(2)=[f(1)]^2-2`

`f(2)=2^2-2`

`f(2)=2`

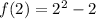
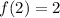
Thus, the value of f(2) is 2.

The value of f(3):

The value of f(3) can be determined by substituting n = 3 in the function
`f(n)=[f(n-1)]^2-n`

Thus, we get;

`f(3)=[f(3-1)]^2-3`

`f(3)=[f(2)]^2-3`

`f(3)=2^2-3`

`f(3)=1`

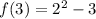
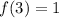
Thus, the value of f(3) is 1.

The value of f(4):

The value of f(4) can be determined by substituting n = 4 in the function
`f(n)=[f(n-1)]^2-n`

Thus, we get;

`f(4)=[f(4-1)]^2-4`

`f(4)=[f(3)]^2-4`

`f(4)=1^2-4`

`f(4)=-3`

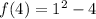
Thus, the value of f(4) is -3.