Answer:
(a) The mass remains after t years is
 mg.
mg.
(b)Therefore the remains sample after 120 years is 11.25 mg.
(c)Therefore after 224.76 years only 1 mg will remain.
Explanation:
The differential equation of decay
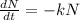
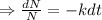
Integrating both sides

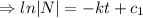
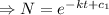 [
[
 is arbitrary constant ]
is arbitrary constant ]
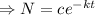
![[ e^(c_1)=c ]](https://img.qammunity.org/2021/formulas/mathematics/college/p6pu5g5uy64sirqz6f0w6atge8bn79bzio.png)
Initial condition is,
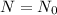 when t=0
when t=0
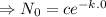
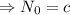
Therefore
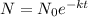 ........(1)
........(1)
N= Amount of radioactive material after t unit time.
 = initial amount of radioactive material
= initial amount of radioactive material
k= decay constant.
Half life:
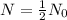 , t= 30 years
, t= 30 years
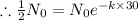

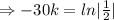
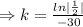
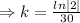
(a)
The mass remains after t years N.
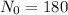
Now we put the value of
 in the equation (1)
in the equation (1)
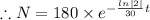
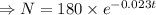 .........(2)
.........(2)
The mass remains of cesium after t years is
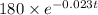 mg.
mg.
(b)
Putting
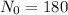 and t=120 years in equation (2)
and t=120 years in equation (2)
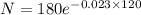
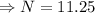
Therefore the remains sample after 120 years is 11.25 mg.
(c)
Now putting N= 1 in equation (2)
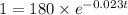
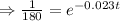
Taking ln both sides
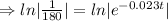
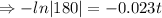
⇒t=224.76 (approx)
Therefore after 224.76 years only 1 mg will remain.