Question

Two basketballs of equal mass are rolling toward each other at constant velocities. The first basketball (B1) has a velocity of 4.3 m/s, and the second basketball (B2) has a velocity of -4.3 m/s.

If these basketballs have a perfectly elastic collision, B1 will have a final velocity of _______, and B2 will have a final velocity

Answer 1

`v'_2 = (2m_1)/(m_1+m_2) (4.3) - (m_1-m_2)/(m_1+m_2) (4.3)\\\\v'_1 = (m_1-m_2)/(m_1+m_2) (4.3) + (2m_2)/(m_1+m_2) (4.3)`

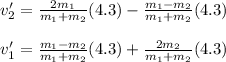
Step-by-step explanation:

Velocity of B₁ = 4.3m/s

Velocity of B₂ = -4.3m/s

For perfectly elastic collision:, momentum is conserved

`m_1v_1 + m_2v_2 = m_1v'_1 + m_2v'_2`

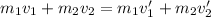
where,

m₁ = mass of Ball 1

m₂ = mass of Ball 2

v₁ = initial velocity of Ball 1

v₂ = initial velocity of ball 2

v'₁ = final velocity of ball 1

v'₂ = final velocity of ball 2

The final velocity of the balls after head on elastic collision would be

`v'_2 = (2m_1)/(m_1+m_2) v_1 - (m_1-m_2)/(m_1+m_2) v_2\\\\v'_1 = (m_1-m_2)/(m_1+m_2) v_1 + (2m_2)/(m_1+m_2) v_2`

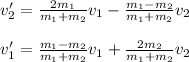
Substituting the velocities in the equation

`v'_2 = (2m_1)/(m_1+m_2) (4.3) - (m_1-m_2)/(m_1+m_2) (4.3)\\\\v'_1 = (m_1-m_2)/(m_1+m_2) (4.3) + (2m_2)/(m_1+m_2) (4.3)`

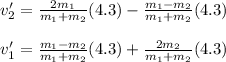
If the masses of the ball is known then substitute the value in the above equation to get the final velocity of the ball.