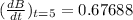Question

I really need help with this calculus 1 question?

Answer 1

a) The rate of change brightness after 't' years

`(dB)/(dt) = 5.0+0.55cos( (2\pi(t) )/(4.7))((2\pi )/(4.7))`

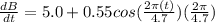
b) The rate of increase after five years

`((dB)/(dt))_(t=5) = 0.67688`

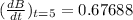
Explanation:

a) Given B(t) = 5.0+0.55sin(
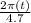`(2\pi(t) )/(4.7)` .....(1)

The rate of change of the brightness after 't' days that is

`(dB)/(dt)`

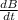
now differentiating equation (1) with respective to 't'

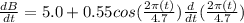`(dB)/(dt) = 5.0+0.55cos( (2\pi(t) )/(4.7))(d)/(dt) ((2\pi(t) )/(4.7))` { using d/dx(sin x) =cos x}

`(dB)/(dt) = 5.0+0.55cos( (2\pi(t) )/(4.7))((2\pi )/(4.7))`

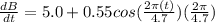
b) The rate of increase after five days

substitute t = 5 in equation dB/d t

`(dB)/(dt) = 5.0+0.55cos( (2\pi(5) )/(4.7))((2\pi )/(4.7))`

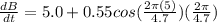
after calculation
`((dB)/(dt))_(t=5) = 0.67688`