Question

Ask Your Teacher Quantitative noninvasive techniques are needed for routinely assessing symptoms of peripheral neuropathies, such as carpal tunnel syndrome (CTS). An article reported on a test that involved sensing a tiny gap in an otherwise smooth surface by probing with a finger; this functionally resembles many work-related tactile activities, such as detecting scratches or surface defects. When finger probing was not allowed, the sample average gap detection threshold for m = 5 normal subjects was 1.97 mm, and the sample standard deviation was 0.56; for n = 12 CTS subjects, the sample mean and sample standard deviation were 2.58 and 0.88, respectively. Does this data suggest that the true average gap detection threshold for CTS subjects exceeds that for normal subjects? State and test the relevant hypotheses using a significance level of 0.01. (Use μ1 for normal subjects and μ2 for CTS subjects.)

Answer 1

Explanation:

Hello!

To test the effectiveness of a noninvasive technique for detecting a tiny gap in a smooth surface by proving it with a finger, two samples were taken:

Sample 1

X₁: gap detection threshold for a normal subject

n₁= 5

X[bar]₁= 1.97 mm

S₁= 0.56

Sample 2

X₂: gap detection threshold for a person with carpal tunnel syndrome (CTS)

n₂= 12

X[bat]₂= 2.58

S₂= 0.88

You have to test if the average gap detection threshold fro CTS subjects is greater than the average gap detection threshold of normal subjects, symbolically: μ₁ < μ₂

The hypotheses are:

H₀: μ₁ ≥ μ₂

H₁: μ₁ < μ₂

α: 0.01

Assuming that both variables come from normal populations and both population variances are equal, the statistic for this test is a t-test for two independent samples with pooled sample variance:

`t= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{Sa*\sqrt{(1)/(n_1) +(1)/(n_2) } } ~t_(n_1+n_2-2)`

`Sa= \sqrt{((n_1-1)S_1^2+(n_2-1)S_2^2)/(n_1+n_2-2) } = \sqrt{(4*0.56^2+11*0.88^2)/(5+12-2) }= 0.81`

`t_(H_0)= \frac{(1.97-2.58)-0}{0.81*\sqrt{(1)/(5) +(1)/(12) } } = -1.41`

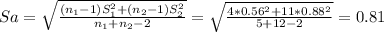
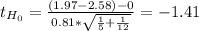
This test is one-tailed to the left and so is the p-value:

P(t₁₅≤-1.41)= 0.0895

Since the p-value:0.0895 is greater than the significance level α:0.01 the decision is to not reject the null hypothesis.

At a 1% significance level, there is no evidence that the true average of the gap detection threshold of subjects with CTS is greater than the true average of gap detection threshold of normal subjects.

I hope you have a SUPER day!