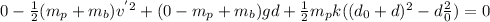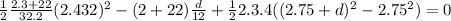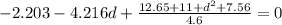Answer:
Step-by-step explanation:
the putty (W
 = 2.3lb) strikes the block with velocity ( here h = 8.7ft):
= 2.3lb) strikes the block with velocity ( here h = 8.7ft):
V
 =
=
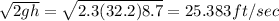
conservation of linear momentum gives (where W
 = 22lb):
= 22lb):
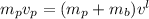
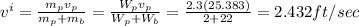
since k = 4lb/in and there are two springs, the initial spring deflection is
δ
 =
=
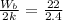 = 2.75in
= 2.75in
conservation of energy gives (datum is the initial position of the block and we divide with 12 to get deflection in inches):
ΔT + ΔV
 + ΔV
+ ΔV
 = 0
= 0