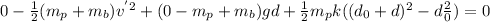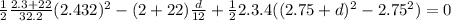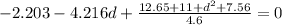Question

The 2.3-lb piece of putty is dropped 8.7 ft onto the 22.0-lb block initially at rest on the two springs, each with a stiffness k = 4.0 lb/in. Calculate the additional deflection δ of the springs due to the impact of the putty, which adheres to the block upon contact.

Answer 1

Step-by-step explanation:

the putty (W
`_(p)` = 2.3lb) strikes the block with velocity ( here h = 8.7ft):

V
`_(p)` =
`√(2gh) = √(2.3(32.2)8.7) = 25.383ft/sec`

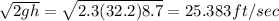
conservation of linear momentum gives (where W
`_(b)` = 22lb):

`m_(p)v_p = (m_(p)+m_(b))v^(l)`

`v^(i) = (m_(p)v_(p))/(m_(p) + m_(b)) =(W_(p)v_(p))/(W_(p)+W_(b)) = (2.3(25.383))/(2+22) =2.432ft/sec`

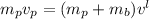
since k = 4lb/in and there are two springs, the initial spring deflection is

δ
`_(0)` =
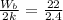`(W_(b))/(2k) = (22)/(2.4)` = 2.75in

conservation of energy gives (datum is the initial position of the block and we divide with 12 to get deflection in inches):

ΔT + ΔV
`_(g)` + ΔV
`_(e)` = 0

`0 - (1)/(2)(m_(p)+m_(b))v^('2) +(0-m_(p)+m_(b))gd+(1)/(2)m_(p)k((d_(0)+d)^(2) - d(2)/(0) ) = 0`

`(1)/(2) (2.3+22)/(32.2) (2.432)^(2) -(2+22)(d)/(12) +(1)/(2)2.3.4((2.75 + d)^(2)-2.75^(2) ) =0`

`-2.203-4.216d+(12.65+11+d^(2)+7.56 )/(4.6) =0`