Question

Suppose the impulse response of an FIR filter of order m 5 5 is as follows where the X terms are to be determined. h 5 f2, 4, 3, X, X, Xg (a) Assuming H(z) is a linear-phase filter, find the complete impulse response. If there are multiple solutions, find each of them.

Answer 1

Explanation:

x  n = e j0n  –   n 

Consider an FIR filter when the input is a complex sinusoid of the form

x  n = Ae^((j)) e^((jn))  –   n 

Where it could be that was obtained by sampling the complex sinusoid

xt  Ae^(j) e^(j0t) and 0=0Ts

From the difference equation for an tap FIR filter,

y_n=∑_(k=0)^5▒〖bxn-k〗

H(e^((j)))= ∑_(k=0)^5▒〖b_k e^((jk)) 〗

Answer 2

Complete Question:

Suppose the impulse response of an FIR filter of order m =5 is as follows where the X terms are to be determined.

h = [2,4,3,X,X,X]

a) Assuming H(z) is a linear- phase filter, find the complete impulse response. If there are multiple solutions, find each of them

b) For each solution in part (a), indicate the linear-phase FIR filter type

c) For each solution in part (a), find the phase offset, α, and the group delay, D(f)

Answer:

a1) For symmetric impulse response, h(n) = [2,4,3,3,4,2]

a2)For asymmetric impulse response h(n) = [2,4,3,-3,-4,-2]

b1) For symmetric impulse response,the FIR filter is a low pass filter

b2) For symmetric impulse response,, the FIR filter is a differentiator

c1) Phase offset = -2.5w

c2) D(f) = π/2 - 2.5w

Explanation:

a) The impulse response, h can either be symmetric or anti-symmetric about α = m/2

i) When the impulse response, h is symmetric about α = m/2, h becomes:

h(n) = [2,4,3,3,4,2]

ii) When the impulse response, h is anti-symmetric about α = m/2, h becomes:

h(n) = [2,4,3,-3,-4,-2]

b) Relationship for converting h(n) into the frequency domain using Fourier transform:
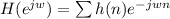`H(e^(jw) ) = \sum h(n) e^(-jwn)`, n= 1,2,3,4,5

i) For h(n) = [2,4,3,3,4,2]

`H(e^(jw) ) = h(0) + h(1) e^(-jwn) + h(2) e^(-2jw) + h(3) e^(-3jw) + h(4) e^(-4jw) + h(5) e^(-5jw)`

`H(e^(jw) ) = 2 + 4 e^(-jw) + 3 e^(-2jw) + 3 e^(-3jw) + 4 e^(-4jw) + 2 e^(-5jw)`

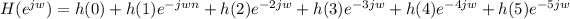
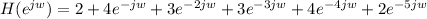
When
`w=0`,
`H(e^(j0)) = 18`

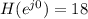
When w = π,
`H(e^(j\pi )) = 0`

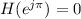
This is the property of a low pass filter, hence the FIR filter is a low pass filter

ii) For h(n) = [2,4,3,-3,-4,-2]

`H(e^(jw) ) = h(0) + h(1) e^(-jwn) + h(2) e^(-2jw) + h(3) e^(-3jw) + h(4) e^(-4jw) + h(5) e^(-5jw)`

`H(e^(jw) ) = 2 + 4 e^(-jw) + 3 e^(-2jw) - 3 e^(-3jw) - 4 e^(-4jw) - 2 e^(-5jw)`

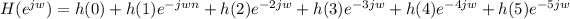
When
`w=0, H(e^(jo)) = 0`

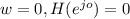
When
`w=\pi , H(e^(j \pi)) = 0`

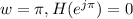
This is the property of a differentiator, hence the FIR filter is a differentiator.

c1) Phase offset = -wα

α = 5/2 = 2.5

Phase offset = -2.5w

c2) Group delay, D(f) = π/2 - αw

D(f) = π/2 - 2.5w