Complete Question:
Suppose the impulse response of an FIR filter of order m =5 is as follows where the X terms are to be determined.
h = [2,4,3,X,X,X]
a) Assuming H(z) is a linear- phase filter, find the complete impulse response. If there are multiple solutions, find each of them
b) For each solution in part (a), indicate the linear-phase FIR filter type
c) For each solution in part (a), find the phase offset, α, and the group delay, D(f)
Answer:
a1) For symmetric impulse response, h(n) = [2,4,3,3,4,2]
a2)For asymmetric impulse response h(n) = [2,4,3,-3,-4,-2]
b1) For symmetric impulse response,the FIR filter is a low pass filter
b2) For symmetric impulse response,, the FIR filter is a differentiator
c1) Phase offset = -2.5w
c2) D(f) = π/2 - 2.5w
Explanation:
a) The impulse response, h can either be symmetric or anti-symmetric about α = m/2
i) When the impulse response, h is symmetric about α = m/2, h becomes:
h(n) = [2,4,3,3,4,2]
ii) When the impulse response, h is anti-symmetric about α = m/2, h becomes:
h(n) = [2,4,3,-3,-4,-2]
b) Relationship for converting h(n) into the frequency domain using Fourier transform:
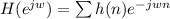 , n= 1,2,3,4,5
, n= 1,2,3,4,5
i) For h(n) = [2,4,3,3,4,2]
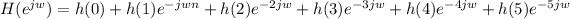
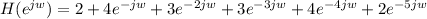
When
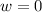 ,
,
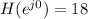
When w = π,
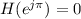
This is the property of a low pass filter, hence the FIR filter is a low pass filter
ii) For h(n) = [2,4,3,-3,-4,-2]
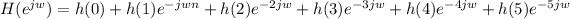
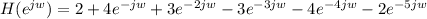
When
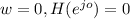
When
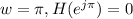
This is the property of a differentiator, hence the FIR filter is a differentiator.
c1) Phase offset = -wα
α = 5/2 = 2.5
Phase offset = -2.5w
c2) Group delay, D(f) = π/2 - αw
D(f) = π/2 - 2.5w