Question

Suppose ff is a continuous function that has critical points at x=-2x = − 2 and at x=1x = 1 such that f'(-2)=0f ′ ( − 2 ) = 0 and f'(1)=0f ′ ( 1 ) = 0. The second derivative of f (x)f ( x ) is given as LaTeX: f''(x) = x^2-4x+1f ″ ( x ) = x 2 − 4 x + 1. Use the second derivative test and choose the correct statement regarding local extrema at the given critical points.

Answer 1

Explanation:

It seems that the question is incomplete and no further information was found on the internet. Nevertheless, it seems that the question is regarding the second derivative criteria.

REcall that the second derivative criteria is used to determine whether a critical point is a minimum or a maximum. A point is called critical if the first derivative is zero or if it doesn't exist at the point.

The criteria is as follows. Given a point
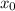`x_0`, provided a function that is twice differentiable, the point is a minimum if and only if
`f''(x_0)>0`, a maximum if and only if
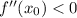`f''(x_0)<0` and an inflexion point if
`f''(x_0)=0`.

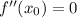Let us use the second derivative criteria to determine if the given points are a maximum, a minimum or inflexion points.

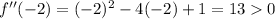`f''(-2) = (-2)^2-4(-2)+1 = 13>0`(this means x=-2 is a minimum)

`f''(1) = (1)^2-4(1)+1 = -2<0`(this means x=1 is a maximum)