Question

Suppose you work in a lab to develop a robotic fish that can swim at various depths of the ocean. A part of the robotic fish can be considered as a metal block that is exposed to the compressive pressure p that the water exerts on all sides of the block. Besides the compressive pressure p, the only other stress that the metal block is subject to is a shear stress loading Txy. Hence, the other two shear stresses are zero ( Txz = Tyz = 0). The yield strength of this metal is 0. = 300 MPa.

(a) Suppose the robotic fish swims in a depth of the ocean where the water pressure loading is p= 90 MPa. Use the Octahedral Shear Stress Yield Criterion (i.e. the von Mises Yield Criterion) to determine the largest value of Txy that can be apply if we want a safety factor against yielding of X.= 1.5?
(b) Suppose the robotic fish then swims in a depth where the water pressure loading is 20 times more, i.e. p = 1,800 MPa. Use the Octahedral Shear Stress Yield Criterion (i.e. the von Mises Yield Criterion) to determine the largest value of Txy that can be apply if we want a safety factor against yielding of Xo = 1.5 ?

Answer 1

a) txy = 1115.5 MPa

b) oy is independent of pressure, thus txy=1115.5 MPa

Step-by-step explanation:

The stress tensor is:

`o=\left[\begin{array}{ccc}-p&t&0\\t&-p&0\\0&0&-p\end{array}\right]`

where p is the pressure, t is the shear stress

`oy=\sqrt{(oxx^(2)+oyy^(2)+ozz^(2)-oxxoyy-oyyozz-ozzoxx)+3(txy^(2)+tyz^(2)+tzx^(2) }`

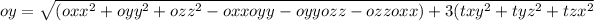
substituting the matrix values:

`oy=\sqrt{p^(2)+p^(2)+p^(2)-p^(2)-p^(2)-p^(2)+3(t^(2)+0+0) } =√(3) t`

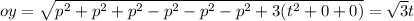
a)
`oy=(oo)/(F) =√(3) t=(300)/(1.5)`

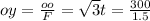
Clearing t:

t=1115.5 MPa = txy

b) oy is independent of pressure, thus txy=1115.5 MPa