Question

Which represents the inverse of the function f(x) = 4x?

h(x) = x + 4
h(x) = x – 4
h(x) = three-quartersx
h(x) = one-quarterx
Mark this and return

Answer 1

d

Step-by-step explanation:

correct edge2020

Answer 2

Option D:
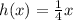`h(x)=(1)/(4)x` is the inverse of the function f(x) = 4x

Step-by-step explanation:

Given that the function is
`f(x)=4x`

We need to determine the inverse of the function.

Inverse of the function h(x):

The inverse of the function can be determined by interchanging the variables x and y and then solving the function for y.

Thus, the function is written as,

`y=4x`

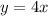
Interchanging the variables x and y, we have;

`x=4y`

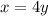
Dividing both sides by 4, we get;

`(1)/(4)x=y`

Thus, the inverse of the function is
`h(x)=(1)/(4)x`

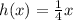
Hence, Option D is the correct answer.