Question

A clinical trial tests a method designed to increase the probability of conceiving a girl. In the study 580 babies were​ born, and 319 of them were girls. Use the sample data to construct a 99​% confidence interval estimate of the percentage of girls born. Based on the​ result, does the method appear to be​ effective? nothingless than pless than nothing ​(Round to three decimal places as​ needed.)

Answer 1

No, Method is not effective.

Explanation:

Let x be the number of girls = 319

and n be the total number of babies = 580

Then, proportion

`\hat{p}=(p)/(n)\\\\=(310)/(580)\\\\=0.55`

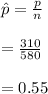
Standard Error,

`SE = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\= \sqrt{(0.55(1-0.55))/(580)}\\= 0.02066`

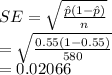
The level of significance is:

`Z_{(\alpha)/(2)}=Z_(0.005)=2.575`

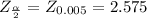
Confidence Interval:

`p \pm [Z_{(\alpha)/(2)} * SE]\\=0.550 \pm [2.575 * 0.02066\\=(0.4968, 0.6032)`

Since 0.50 lies in the interval hence we fail to reject

`H_0: p = 0.50`

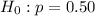
Thus, the method does not appear to be effective.