Question

Problem 2. Electric Heating of a Room An air-tight room contains 80 kg of air, and a 2-kW baseboard electric resistance heater in the room is turned on and kept on for 15 min. Calculate the temperature rise of air at the end of 15 min.

Answer 1

The temperature rise of air at the end of 15 min is
`31.34`°C

Step-by-step explanation:

Data

`t=15min, t=15*60sec, t=900seconds`

`W=2kW`

`m=80kg`

`constant c_(v)`=0.718

We can use energy balance to solve the problem.

The energy balance stated that:

`W=`Δ
`U`

`W=mc_(v)`Δ
`T`

`W=(m)/(t) c_(v)`Δ
`T`

we can now make ΔT the subject of the formula

ΔT
`=(W*t)/(mc_(v) )`

substitute the values

ΔT
`=(2*900)/(80*0.718)`

ΔT=
`=31.34`°C

Answer 2

The rise in temperature after 15mins is (ΔT)=
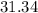`31.34`°c

Step-by-step explanation:

The solution is obtained from energy balance;

W=M x Cv x ΔT

where;

W(workdone)=quantity of energy in joules

Workdone=Power x Time

Power=2kw

Time=15mins=15 x 60=900secs

Workdone=2 x 900=1800KJ

Cv=Specific heat capacity of air= 0.718 kJ/kg.K

M=Mass of air=80kg

ΔT= change in temperature in °C

therefore;

ΔT=
`(W)/(Cv *M)`

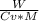
ΔT=
`(1800)/(0.718*80)`

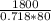
ΔT=
`(1800)/(57.44)`

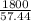
ΔT=
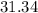`31.34`°c