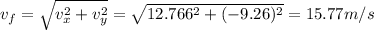Question

As an aid in working this problem, consult Interactive Solution 3.41. A soccer player kicks the ball toward a goal that is 25.0 m in front of him. The ball leaves his foot at a speed of 16.2 m/s and an angle of 38.0 ° above the ground. Find the speed of the ball when the goalie catches it in front of the net.

Answer 1

15.77m/s

Step-by-step explanation:

the information we have is:

initial velocity
`v_(0)=16.2m/s`

distance:
`d=25m`

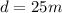
angle:
`\theta=38`°

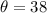first we need to break down the velocity into its x and y components:

initial velocity in x (the velocity in x is constant):

`v_(0x)=v_(0)cos\theta\\v_(0x)=(16.2m/s)cos38\\v_(0x)=12.766m/s`

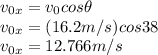
and initial velocity in y (the velocity in y is not constant due to acceleration of gravity):

`v_(0y)=v_(0)sin\theta\\v_(0y)=(16.2m/s)sin38\\v_(0y)=9.97m/s`

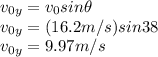
and now we find the time that the ball was in the air:

`t=(d)/(v_(0x)) =(25m)/(12.766m/s)\\ t=1.96s`

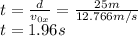
and with this time, we find the y component of the volicity at time 1.96s:

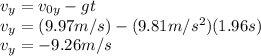`v_(y)=v_(0y)-gt\\v_(y)=(9.97m/s)-(9.81m/s^2)(1.96s)\\v_(y)=-9.26m/s`(negative because it points downward)

finally, to find the final velocity we use pythagoras:

`v_(f)=\sqrt{v_(x)^2+v_(y)^2} =√(12.766^2+(-9.26)^2)=15.77m/s`