Answer:
The test statistic (z-score) of this one-mean hypothesis test is z=1.823.
Explanation:
The null and alternative hypothesis are:
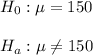
The significance level is 0.05.
The sample size is n=22.
The sample mean is M=157.
The standard deviation is 18.
The z-score can be calculated as:

The test statistic (z-score) of this one-mean hypothesis test is z=1.823.