Answer:
the force required are
- Fx = - 523.5 Ibf ( x axis)
- Fy = - 58.94 Ibf ( y axis)
Step-by-step explanation:
Data given
V2 = V3 = 80.2 ft/s
P1 = 43 psig = 6192 Ib/ft^2
note: P2 = P3 = Patm = 0 Ib/ ft^2
D2 = D3 = 1 inch
D1 = 4 inches
p = 62.4 Ibm/ft3 = 1.94 slug/ft3
calculate the cross sectional Areas of the water jets
A 1 =
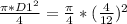 = 0.0873 ft2
= 0.0873 ft2
A2 =
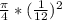 = 0.005454 ft2
= 0.005454 ft2
calculate the mass flow rate
M2 = M3 = P *A2*V2 = 1.94 * 0.005454 * 80.2 = 0.8486 slug/s
calculate the mass balance
M1 = M2 + M2 = 0.8486 + 0.8486 = 1.6972 Ibm/ s
next calculate the velocity at each section
velocity at section 1 of pipe
=
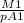
V1 =
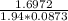 = 10.02 ft/s
= 10.02 ft/s
calculate the linear momentum
F = m ( Vout - Vin )
along the x - direction
Fx + (P1 A1) - (P2 A2) + (P3 A3) sin 30 = (M2 V2) + M3 ( -V3 sin 30) - (M1 V1)
Fx + 540.56 = 68.06 -34.03 - 17
Fx = -523.5 Ibf
Along the y - direction
Fy + P3 A3 COS 30 = M3 ( -V3 COS 30 ) - 0
Fy + 0 = 0.8486 ( -80.2 cos 30 )
Fy = - 58.94 Ibf