Question

Two circular water (???????? = 62.4 lbm/ft3) jets of 1 in. diameter (d = 1 in.) issue from this unusual nozzle. If the efflux speed is 80.2 ft/s, what force is required at the flange to hold the nozzle in place? The pressure in the 4 in. pipe (D = 4 in.) is 43 psig.

Answer 1

the force required are

• Fx = - 523.5 Ibf ( x axis)
• Fy = - 58.94 Ibf ( y axis)

Step-by-step explanation:

Data given

V2 = V3 = 80.2 ft/s

P1 = 43 psig = 6192 Ib/ft^2

note: P2 = P3 = Patm = 0 Ib/ ft^2

D2 = D3 = 1 inch

D1 = 4 inches

p = 62.4 Ibm/ft3 = 1.94 slug/ft3

calculate the cross sectional Areas of the water jets

A 1 =
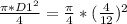`(\pi*D1^(2) )/(4) = (\pi )/(4 )* ( (4)/(12) )^(2)` = 0.0873 ft2

A2 =
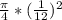`(\pi )/(4) * ( (1)/(12))^(2)` = 0.005454 ft2

calculate the mass flow rate

M2 = M3 = P *A2*V2 = 1.94 * 0.005454 * 80.2 = 0.8486 slug/s

calculate the mass balance

M1 = M2 + M2 = 0.8486 + 0.8486 = 1.6972 Ibm/ s

next calculate the velocity at each section

velocity at section 1 of pipe

=
`(M1)/(pA1)`

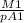
V1 =
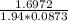`(1.6972)/(1.94 * 0.0873)` = 10.02 ft/s

calculate the linear momentum

F = m ( Vout - Vin )

along the x - direction

Fx + (P1 A1) - (P2 A2) + (P3 A3) sin 30 = (M2 V2) + M3 ( -V3 sin 30) - (M1 V1)

Fx + 540.56 = 68.06 -34.03 - 17

Fx = -523.5 Ibf

Along the y - direction

Fy + P3 A3 COS 30 = M3 ( -V3 COS 30 ) - 0

Fy + 0 = 0.8486 ( -80.2 cos 30 )

Fy = - 58.94 Ibf

Answer 2

Fnet=(3666.47i-8487.33j) lbf

Step-by-step explanation:

The velocity in the nozzle V1 is:

`v_(1)=(Q)/(A)=(`

where Q is the discharge, vj is the velocity in the jet, d is the diameter of the jet and D is the diameter of the nozzle. Replacing values:

`v_(1)=2*80.2(((\pi )/(4)1^(2) )/((\pi )/(4)4^(2) ) )=10.02 fps`

In x-direction the momentum is:

∑Fx=∑m-miVix

`Fx_{}+p_(1)((\pi )/(4)D^(2))=p((\pi )/(4)d^(2))v_(j)^(2)-p((\pi )/(4)d^(2))v_(j)^(2)sin\alpha -p((\pi )/(4)d^(2))v_(1)^(2)`

where

p1=pressure=43 psig

D=4 in=0.33 ft

d=1=0.083 ft

α=30°

p=density=1.94 slug/ft^3

Replacing values and clearing Fx:

Fx=3666.47 lbf

In x-direction the momentum is:

∑Fy=∑m-miViy

`F_(y)=p((\pi )/(4)d^(2) )v_(j)(-v_(j)cos\alpha )`

Replacing previous values, we have:

Fy = -8487.33 lbf

The net force is equal to:

Fnet=Fx+Fy

Fnet=(3666.47i-8487.33j) lbf