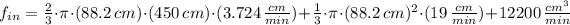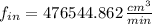Question

Water is leaking out of an inverted conical tank at a rate of 12200 cubic centimeters per min at the same time that water is being pumped into the tank at a constant rate. The tank has height 14 meters and the diameter at the top is 4.5 meters. If the water level is rising at a rate of 19 centimeters per minute when the height of the water is 4.5 meters, find the rate at which water is being pumped into the tank in cubic centimeters per minute.

Answer 1

`f_(in) = 476544.862\,(cm^(3))/(min)`

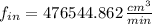
Explanation:

The conical tank is modelled by the Principle of Mass Conservation:

`\dot m_(in) - \dot m_(out) = (dm_(tank))/(dt)`

As water is an incompressible fluid, the equation can be simplified into this:

`f_(in) - f_(out) = (dV_(tank))/(dt)`

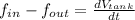
The rate at which water is being pumped into the tank is:

`f_(in) = (dV_(tank))/(dt) + f_(out)`

`f_(in) = (2)/(3)\cdot \pi \cdot r\cdot h \cdot (dr)/(dt) + (1)/(3)\cdot \pi \cdot r^(2)\cdot (dh)/(dt) + f_(out)`

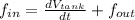
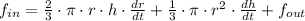
The cone obeys the following relationship:

`(r)/(h) = (2.75\,m)/(14\,m)`

`r = 0.196\cdot h`

`r = 0.196\cdot (450\,cm)`

`r = 88.2\,cm`

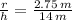
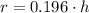
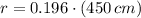
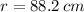
By deriving the expression:

`(dr)/(dt) = 0.196\cdot (dh)/(dt)`

`(dr)/(dt) = 0.196\cdot (19\,(cm)/(min) )`

`(dr)/(dt) = 3.724\,(cm)/(min)`

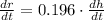
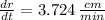
The flow required to be pumped is:

`f_(in) = (2)/(3)\cdot \pi \cdot (88.2\,cm)\cdot (450\,cm) \cdot (3.724\,(cm)/(min) )+(1)/(3)\cdot \pi \cdot (88.2\,cm)^(2)\cdot (19\,(cm)/(min) )+12200\,(cm^(3))/(min)`

`f_(in) = 476544.862\,(cm^(3))/(min)`