Question

A professor claims that his students' average score on the first exam of the semester is different than the average score on the second exam. The professor has several large classes, so he selects a random sample of students and compares their scores on the two exams. Suppose that data were collected for a random sample of 8 students, where each difference is calculated by subtracting the percentage score from the second exam from the percentage score of the first exam. Assume that the populations are normally distributed. Using a test statistic of t≈0.704, the significance level α=0.01, and the corresponding p-value greater than 0.10, draw a conclusion for the appropriate hypothesis test, where the null hypothesis is H0:μd=0 and the alternative hypothesis is Ha:μd≠0.

Answer 1

`t=(\bar d -0)/((s_d)/(√(n)))=0.704`

`p_v = 2*P(t_(7) >0.704)=0.504`

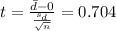
So the p value is higher the significance level given 0.1, so then we can conclude that we FAIL to reject the null hypothesis that the difference mean between after and before score is equal 0. So then we don't have enough evidence to say that the score for the second exam is different than the score for the first exam.

Explanation:

Previous concepts

A paired t-test is used to compare two population means where you have two samples in which observations in one sample can be paired with observations in the other sample. For example if we have Before-and-after observations (This problem) we can use it.

Let put some notation

x=test value before (first exam) , y = test value after (second exam)

The system of hypothesis for this case are:

Null hypothesis:
`\mu_y -\mu_x =0`

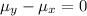
Alternative hypothesis:
`\mu_y -\mu_x \\eq 0`

The first step is calculate the difference
`d_i=y_i-x_i`

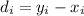
The statistic given by :

`t=(\bar d -0)/((s_d)/(√(n)))=0.704`

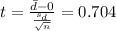
The next step is calculate the degrees of freedom given by:

`df=n-1=8-1=7`

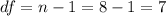
Now we can calculate the p value, since we have a left tailed test the p value is given by:

`p_v = 2*P(t_(7) >0.704)=0.504`

So the p value is higher the significance level given 0.1, so then we can conclude that we FAIL to reject the null hypothesis that the difference mean between after and before score is equal 0. So then we don't have enough evidence to say that the score for the second exam is different than the score for the first exam.