Complete question:
A structural component in the form of a wide plate is to be fabricated from a steel alloy that has a plane strain fracture toughness of 98.9 MPa root m (90 ksi root in.) and a yield strength of 860 MPa (125,000 psi). The flaw size resolution limit of the flaw detection apparatus is 3.0 mm (0.12 in.). If the design stress is one-half of the yield strength and the value of Y is 1.0, determine whether or not a critical flaw for this plate is subject to detection.
Answer:
Since the flaw 17mm is greater than 3 mm the critical flaw for this plate is subject to detection
so that critical flow is subject to detection
Step-by-step explanation:
We are given:
Plane strain fracture toughness K
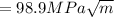
Yield strength Y = 860 MPa
Flaw detection apparatus = 3.0mm (12in)
y = 1.0
Let's use the expression:
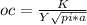
We already know
K= design
a = length of surface creak
Since we are to find the length of surface creak, we will make "a" subject of the formula in the expression above.
Therefore
![a= (1)/(pi) * [(k)/(y*a)]^2](https://img.qammunity.org/2021/formulas/engineering/college/pnlx2qsvydtd3lrwt193vrh5kr8l55n7pf.png)
Substituting figures in the expression above, we have:
![= (1)/(pi) * [\frac{98.9 MPa √(m)} {10 * (860MPa)/(2)}]^2](https://img.qammunity.org/2021/formulas/engineering/college/8hvwr4dvo2ozdpqy1vuww1aosiln58hn2h.png)
= 0.0168 m
= 17mm
Therefore, since the flaw 17mm > 3 mm the critical flow is subject to detection