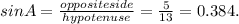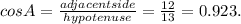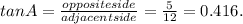Question

Please help with these 2

Answer 1

For the first triangle, sin A = 0.6, cos A = 0.8, tan A = 0.75, sin B = 0.8, cos B = 0.6, and tan B = 1.333.

For the second triangle, sin A = 0.384, cos A = 0.923, tan A = 0.416.

Explanation:

Step 1:

`sin \theta = (oppositeside)/(hypotenuse),`
`cos \theta = (adjacentside)/(hypotenuse),`
`tan \theta = (oppositeside)/(adjacentside).`

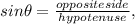
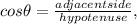
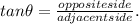
These are the formulae needed to solve the two questions.

Step 2:

For the first triangle, for angle A, the opposite side measures 6 units, the adjacent side measures 8 units while the hypotenuse measures 10 units.

So
`sinA = (oppositeside)/(hypotenuse) = (6)/(10) = 0.6.`

`cosA = (adjacentside)/(hypotenuse) = (8)/(10) = 0.8.`

`tan A = (oppositeside)/(adjacentside) = (6)/(8) = 0.75.`

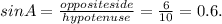
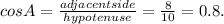
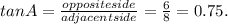
Step 3:

For the first triangle, for angle B, the opposite side measures 8 units, the adjacent side measures 6 units while the hypotenuse measures 10 units.

So
`sinB = (oppositeside)/(hypotenuse) = (8)/(10) = 0.8.`

`cosB = (adjacentside)/(hypotenuse) = (6)/(10) = 0.6.`

`tan B = (oppositeside)/(adjacentside) = (8)/(6) = 1.333.`

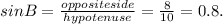
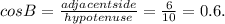
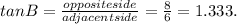
Step 4:

For the second triangle, we need to determine the length of the unknown side.

According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Assume the length of the unknown side is x.

`13^(2) = 12^(2) +x^(2) , x^(2) = 25, x =5.`

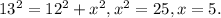
Step 5:

For the second triangle, for angle A, the opposite side measures 5 units, the adjacent side measures 12 units while the hypotenuse measures 13 units.

So
`sinA = (oppositeside)/(hypotenuse) = (5)/(13) = 0.384.`

`cosA = (adjacentside)/(hypotenuse) = (12)/(13) = 0.923.`

`tan A = (oppositeside)/(adjacentside) = (5)/(12) = 0.416.`