Question

The general form of the equation of a circle is x2+y2+2x−6y+1=0.

What are the coordinates of the center of the circle?



Enter your answer in the boxes.

Answer 1

Hello! Really sorry I am late! Hope this helps though! Have a nice day! Really helpful for k12 users!

Explanation:

Answer 2

The answer to your question is Center: (-1 , 3)

Explanation:

Data

x² + y² + 2x - 6y + 1 = 0

Process

1.- Group like terms pass the independent term to the right side

(x² + 2x ) + (y² - 6y ) = -1

2.- Divide the second term of each group by 2 and write the result in the third position of each group to the second power. Write these numbers also in the right side of the equation.

(x² + 2x + (1)²) + (y² - 6y + (3)²) = -1 + (1)² + (3)²

3.- Factor in the left side and simplify in the right side

(x + 1)² + (y - 3)² = -1 + 1 + 9

4.- Simplify

(x + 1)² + (y - 3)² = 9

5.- Find the center and the radius

Center: (-1 , 3)

radius =
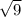`√(9)` = 3