Answer : The pH at equivalence is, 9.21
Explanation : Given,
Concentration of
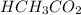 = 0.5870 M
= 0.5870 M
Volume of
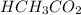 = 90.0 mL = 0.09 L (1 L = 1000 mL)
= 90.0 mL = 0.09 L (1 L = 1000 mL)
First we have to calculate the moles of
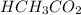
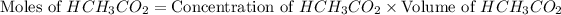
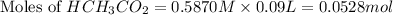
As we known that at equivalent point, the moles of
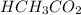 and NaOH are equal.
and NaOH are equal.
So, Moles of NaOH = Moles of
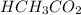 = 0.0528 mol
= 0.0528 mol
Now we have to calculate the volume of NaOH.
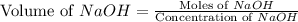
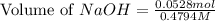
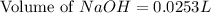
Total volume of solution = 0.09 L + 0.0253 L = 0.1153 L
Now we have to calculate the concentration of KCN.
The balanced equilibrium reaction will be:
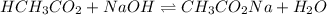
Moles of
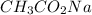 = 0.0528 mol
= 0.0528 mol
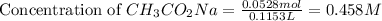
At equivalent point,
![pH=(1)/(2)[pK_w+pK_a+\log C]](https://img.qammunity.org/2021/formulas/chemistry/college/cvxc4ri024tdu4yedmekcr3wix0gtv39cv.png)
Given:
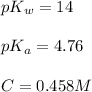
Now put all the given values in the above expression, we get:
![pH=(1)/(2)[14+4.76+\log (0.458)]](https://img.qammunity.org/2021/formulas/chemistry/college/xa85gqappj52gp3al3os02dmu7i80qi955.png)
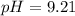
Therefore, the pH at equivalence is, 9.21