Question

A chemist titrates 90.0 mL of a 0.5870 M acetic acid (HCH3CO2) solution with 0.4794M NaOH solution at 25 °C. Calculate the pH at equivalence. The p Kg of acetic acid is 4.76. Round your answer to 2 decimal places.

Answer 1

Answer : The pH at equivalence is, 9.21

Explanation : Given,

Concentration of
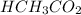`HCH_3CO_2` = 0.5870 M

Volume of
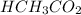`HCH_3CO_2` = 90.0 mL = 0.09 L (1 L = 1000 mL)

First we have to calculate the moles of
`HCH_3CO_2`

`\text{Moles of }HCH_3CO_2=\text{Concentration of }HCH_3CO_2* \text{Volume of }HCH_3CO_2`

`\text{Moles of }HCH_3CO_2=0.5870M* 0.09L=0.0528mol`

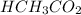
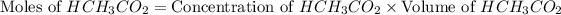
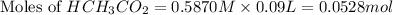
As we known that at equivalent point, the moles of
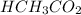`HCH_3CO_2` and NaOH are equal.

So, Moles of NaOH = Moles of
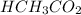`HCH_3CO_2` = 0.0528 mol

Now we have to calculate the volume of NaOH.

`\text{Volume of }NaOH=\frac{\text{Moles of }NaOH}{\text{Concentration of }NaOH}`

`\text{Volume of }NaOH=(0.0528mol)/(0.4794M)`

`\text{Volume of }NaOH=0.0253L`

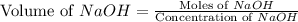
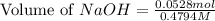
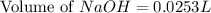
Total volume of solution = 0.09 L + 0.0253 L = 0.1153 L

Now we have to calculate the concentration of KCN.

The balanced equilibrium reaction will be:

`HCH_3CO_2+NaOH\rightleftharpoons CH_3CO_2Na+H_2O`

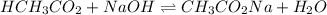
Moles of
`CH_3CO_2Na` = 0.0528 mol

`\text{Concentration of }CH_3CO_2Na=(0.0528mol)/(0.1153L)=0.458M`

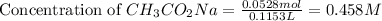
At equivalent point,

`pH=(1)/(2)[pK_w+pK_a+\log C]`

Given:

`pK_w=14\\\\pK_a=4.76\\\\C=0.458M`

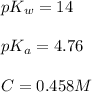
Now put all the given values in the above expression, we get:

`pH=(1)/(2)[14+4.76+\log (0.458)]`

`pH=9.21`

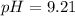
Therefore, the pH at equivalence is, 9.21