The greater root is -4.
Explanation:
- The given equation is
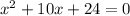
- This a quadratic equation which can be solved using the factorizing method.
- The general form of the quadratic equation is given by
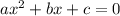
where,
- a is the coefficient of x².
- b is the coefficient of x.
- c is the constant term.
In the given equation, a = 1, b = 10, c = 24.
- Sum of the roots ⇒ b
- Product of the roots ⇒ c
To find the roots of the equation
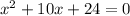 :
:
- Sum of the roots ⇒ 6+4 = 10 (where b = 10).
- Product of the roots ⇒ 6×4 = 24 (where c = 24).
The solution is given by (x+6)(x+4) = 0.
The roots are given by (x+6) = 0 and (x+4) = 0.
Therefore, x= -6 and x = -4 are the roots of the equation
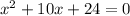
The greater root is -4.