\begin{equation}\text { Question: If } \ln (x+y)=4 * y \text {. Find } (d^(2) y)/(d x^(2)) \text { at } x=0 \text {. }\end{equation}

Question

`\begin{equation}\text { Question: If } \ln (x+y)=4 * y \text {. Find } (d^(2) y)/(d x^(2)) \text { at } x=0 \text {. }\end{equation}`

Answer 1

I think you meant to say

`\ln(x+y) = 4xy`

and not "4 times y" on the right side (which would lead to a complex value for y when x = 0). Note that when x = 0, the equation reduces to ln(y) = 0, so that y = 1.

Implicitly differentiating both sides with respect to x, taking y = y(x), and solving for dy/dx gives

`(1+(dy)/(dx))/(x+y) = 4y + 4x(dy)/(dx)`

`\implies (dy)/(dx) = (4xy+4y^2-1)/(1-4x^2-4xy)`

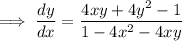
Note that when x = 0 and y = 1, we have dy/dx = 3.

Differentiate both sides again with respect to x :

`(d^2y)/(dx^2) = ((1-4x^2-4xy)\left(4y+4x(dy)/(dx)+8y(dy)/(dx)\right)-(4xy+4y^2-1)\left(-8x-4y-4x(dy)/(dx)\right))/((1-4x^2-4xy)^2)`

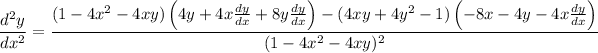
No need to simplify; just plug in x = 0, y = 1, and dy/dx = 3 to get

`(d^2y)/(dx^2) \bigg|_(x=0) = \boxed{40}`