Answer: 12 ft/s
Explanation:
We are told the following function models Spot's height at time
 :
:
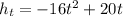 (1)
(1)
And we are asked to find Spot's average rate of ascent, this means its velocity
 , which is calculated by:
, which is calculated by:
 (2)
(2)
Where:
 is the height of Spot at time
is the height of Spot at time
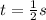
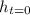 is the height of Spot at time
is the height of Spot at time

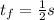 is the final time
is the final time
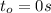 is the initial time
is the initial time
So, firstly we need to calculate
 and
and
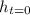 :
:
 (3)
(3)
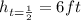 (4)
(4)
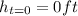 (5)
(5)
Substituting these values in (2):
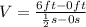 (6)
(6)
Finally:
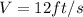 This is Spot's average rate of ascent
This is Spot's average rate of ascent