Answer:
 .
.
Explanation:
Let x represent height of the cone.
We have been given that Sand pouring from a chute forms a conical pile whose height is always equal to the diameter.
We know that radius is half the diameter, so radius of cone would be
 .
.
We will use volume of cone formula to solve our given problem.

Upon substituting the value of height and radius in terms of x, we will get:
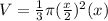
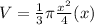

Now, we will take the derivative of volume with respect to time as:
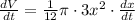
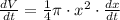
Upon substituting
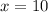 and
and
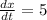 , we will get:
, we will get:
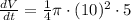
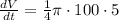

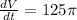
Therefore, the sand is pouring from the chute at a rate of
 .
.