Question

Is equivalent to (RootIndex 3 StartRoot 125 EndRoot) Superscript x?

125 Superscript one-third x

125 Superscript StartFraction 1 Over 3 x EndFraction

125 Superscript 3 x

125 Superscript (one-third) SuperSuperscript x

Answer 1

The answer is a on edge 125 Superscript one-third x

Explanation:

Answer 2

Option a) 125 Superscript one-third x is correct

The equivalent expression to the given expression
`\sqrt[3]{125}^x` is
`(125)^{(1)/(3)x}`

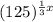
Explanation:

Given that (RootIndex 3 StartRoot 125 EndRoot) Superscript x

Given expression can be written as

`\sqrt[3]{125}^x`

To find the equivalent expression to the given expression :

`\sqrt[3]{125}^x`

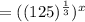`=((125)^{(1)/(3)})^x` ( by using the property
`\sqrt[x]{y}=y^{(1)/(x)}` )

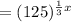`=(125)^{(1)/(3)x}` ( by using the property
`(a^m)^n=a^(mn)` )

`\sqrt[3]{125}^x=(125)^{(1)/(3)x}`

Therefore the equivalent expression to the given expression
`\sqrt[3]{125}^x` is
`(125)^{(1)/(3)x}`

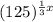
Therefore the equivalent expression to the given expression is 125 Superscript one-third x

Therefore option a) 125 Superscript one-third x is correct.