Question

A segment with endpoints (3,7) and (–8,7) is rotated around the origin. How long will the new segment be?

Answer 1

The relative distance or length remains unchanged.

Step-by-step explanation:

Rotating an image does not change its dimensions, only its position within a coordinate system.

We can show this by rotating the line segment counter-clockwise about the origin through an angle π/2

A rotation of π /2 counter-clockwise maps:

( x , y ) → ( y , - x )

Using given points:

(3,7) → ( 7, -3 )

(–8,7) → (7,8)

Using the distance formula, with coordinates (3,7) and (–8,7)

`d = √((3 - (-8))^2 + (7-7)^2) = 11`

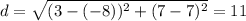
Using the distance formula, with coordinates (7,-3) and (7,8)

`d = √((7 - 7)^2 + ((-3) - 8)^2) = 11`

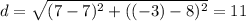
Therefore, the relative distance or length remains unchanged.