The relative distance or length remains unchanged.
Step-by-step explanation:
Rotating an image does not change its dimensions, only its position within a coordinate system.
We can show this by rotating the line segment counter-clockwise about the origin through an angle π/2
A rotation of π /2 counter-clockwise maps:
( x , y ) → ( y , - x )
Using given points:
(3,7) → ( 7, -3 )
(–8,7) → (7,8)
Using the distance formula, with coordinates (3,7) and (–8,7)
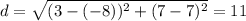
Using the distance formula, with coordinates (7,-3) and (7,8)
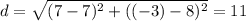
Therefore, the relative distance or length remains unchanged.