Question

In PQR shown below, which expression can be used to find PQ?

Answer 1

Option C:

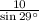`(10)/(\sin 29^(\circ))` can be used to find the length of PQ.

Solution:

Given PQR is a right triangle.

θ = m∠Q = 29°

Opposite of θ = PR = 10

Hypotenuse = PQ = ?

To find the length of PQ:

Using trigonometric ratio formula:

`$\sin \theta=\frac{\text { Opposite side of } \theta}{\text { Hypotenuse }}`

`$\sin \theta=(PR)/(PQ)`

`$\sin 29^\circ=(10)/(PQ)`

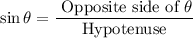
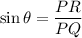
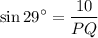
Multiply by PQ on both sides.

`$PQ * \sin 29^\circ=(10)/(PQ) * PQ`

`$PQ * \sin 29^\circ=10`

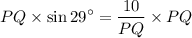
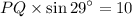
Divide by sin 29° on both sides.

`$(PQ * \sin 29^\circ)/( \sin 29^\circ) =(10)/( \sin 29^\circ)`

`$PQ=(10)/( \sin 29^\circ)`

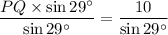
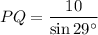
Therefore
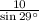`(10)/(\sin 29^(\circ))` can be used to find the length of PQ.

Option C is the correct answer.