Option C:
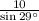 can be used to find the length of PQ.
can be used to find the length of PQ.
Solution:
Given PQR is a right triangle.
θ = m∠Q = 29°
Opposite of θ = PR = 10
Hypotenuse = PQ = ?
To find the length of PQ:
Using trigonometric ratio formula:
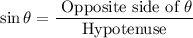
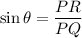
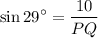
Multiply by PQ on both sides.
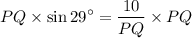
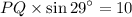
Divide by sin 29° on both sides.
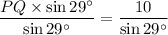
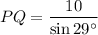
Therefore
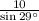 can be used to find the length of PQ.
can be used to find the length of PQ.
Option C is the correct answer.