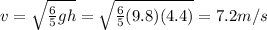Answer:
7.2 m/s
Step-by-step explanation:
We can solve this problem by using the conservation of mechanical energy.
In fact, the initial gravitational potential energy of the sphere when it is at the top is entirely converted into translational kinetic energy + rotational kinetic energy. So we can write:
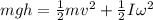 (1)
(1)
where
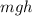 is the gravitational potential energy, with
is the gravitational potential energy, with
m = mass of the sphere
 is the acceleration due to gravity
is the acceleration due to gravity
h = 4.4 m is the initial height of the sphere
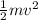 is the translational kinetic energy, where
is the translational kinetic energy, where
v is the final speed of the sphere
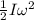 is the rotational kinetic energy, where
is the rotational kinetic energy, where
I is the moment of inertia of the sphere
 is the final angular velocity
is the final angular velocity
For a hollow sphere,
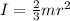
where r is the radius of the sphere. Moreover, we have the following relationship between linear speed and angular velocity:
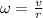
So we can rewrite the rotational kinetic energy as
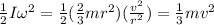
So we can rewrite eq(1) as
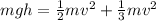
Or equivalently,

And solving for v, we find the final speed of the sphere: