Answer:
The lowest time limit in which 95% of the bugs can be found is 11.22 hours.
Explanation:
We are given that X is the time in hours required to find a bug in a software system. Assume that X is normally distributed with mean of 3 and standard deviation of 5.
So, X = time in hours required to find a bug in a software system
X ~ N(
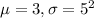 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean value
= mean value
 = standard deviation
= standard deviation
Let the lowest time limit in which 95% of the bugs can be found =

Now, we have to find the lowest time limit in which 95% of the bugs can be found, i.e.;
P(
 <
<
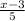 ) = 0.95
) = 0.95
P(Z <
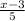 ) = 0.95
) = 0.95
Now, the critical value of
 in the z table which given an area of less than 95% is 1.6449, which means;
in the z table which given an area of less than 95% is 1.6449, which means;
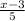 = 1.6449
= 1.6449
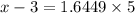
 = 3 + 8.22 = 11.22
= 3 + 8.22 = 11.22
Therefore, the lowest time limit in which 95% of the bugs can be found is 11.22 hours.