Answer:
8 times larger.
Explanation:
The radius of the large sphere is double the radius of the small sphere.
Question asked:
How many times does the volume of the large sphere than the small sphere
Solution:
Let radius of the small sphere =

As the radius of the large sphere is double the radius of the small sphere:
Then, radius of the large sphere =

To find that how many times is the volume of the large sphere than the small sphere, we will divide the volume of large sphere by volume of small sphere:-
For smaller sphere:
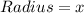
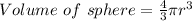
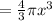
For larger sphere:
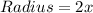
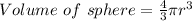
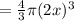
Now, we will divide volume of the larger by the smaller one:
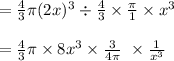
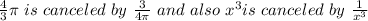
Now, we have
=

Therefore, the volume of the large sphere is 8 times larger than the smaller sphere.